摘要：微分符号揭示了数学中的微妙含义，其中dx与dy是微积分中重要的概念。它们代表着微小的变化量，用于描述函数在某一点的瞬时变化率或斜率。通过微分，我们可以更深入地理解函数的性质和行为，从而解决实际问题。微积分的应用广泛，涉及物理、工程、经济等领域，而微分符号、dx与dy则是这一学科中不可或缺的工具和符号。

本文目录导读：

1. 微分符号
2. dx与dy
3. 微分符号、dx与dy的关系
4. 实际应用

当我们谈论微积分时，一些基本的符号如微分符号、dx和dy经常出现在我们的视线中，这些符号是理解微积分学的核心概念的基础，理解它们的真正含义至关重要，本文将详细探讨微分符号、dx和dy的含义，揭示它们在数学中的微妙之处。

微分符号

微分符号，通常表示为 "d"，在数学中用于表示一个变量的微小变化，在微积分中，微分被用来描述函数在某一点的斜率或函数的局部行为，当我们对一个函数进行微分时，我们实际上是寻找一个表达式，该表达式表示函数值随自变量变化的速率，这种变化率通常被称为导数，微分符号是计算导数的基本工具。

dx与dy

当我们谈论微分时，经常会遇到dx和dy这样的表达，它们到底是什么意思呢？

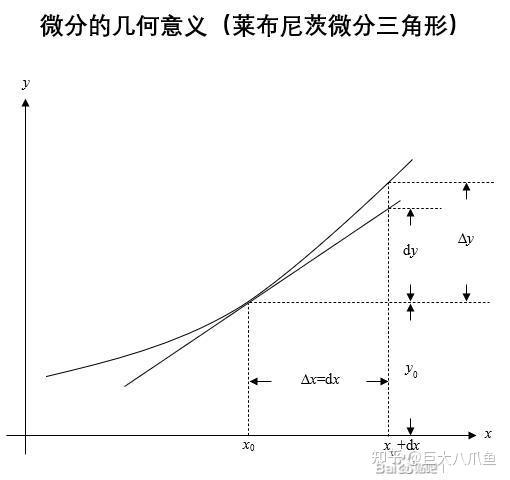
1、dx：dx表示的是自变量的微小变化，在单变量函数中，x通常代表自变量，而dx则表示x的一个微小增量，当我们说“当x从x0变化到x0+dx时”，我们实际上是在描述一个极其微小的变化过程。

2、dy：与dx类似，dy表示的是因变量的微小变化，在一元函数中，y是x的函数，dy则表示y值随x变化的一个微小增量，在微积分中，dy常常与dx配合使用，用于计算函数在某一点的斜率或导数，斜率就是dy/dx，表示函数值y随自变量x变化的速率。

微分符号、dx与dy的关系

微分符号、dx和dy之间的关系密切，它们共同构成了微积分学的核心部分，微分符号帮助我们计算一个函数在某一点的导数，而dx和dy则分别表示自变量和因变量的微小变化，这种关系主要体现在导数的计算中，导数描述的是函数值随自变量变化的速率，而这种速率的计算正是通过比较函数值的微小变化（dy）与自变量的微小变化（dx）来完成的，导数就是dy/dx，表示函数值y随自变量x变化的比率。

实际应用

微分符号、dx和dy在物理学、工程学、经济学等各个领域都有广泛的应用，在物理学中，它们被用于描述运动物体的速度、加速度以及力等概念；在经济学中，这些概念被用于分析成本、收益和市场需求等问题；在工程学中，它们被用于优化设计、优化路径等问题，这些应用都涉及到对微小变化的精确描述和计算，理解微分符号、dx和dy的含义至关重要。

本文详细探讨了微分符号、dx和dy的含义及其在微积分中的应用，这些符号是理解微积分学的核心概念的基础，因此理解它们的真正含义至关重要，通过本文的阐述，我们了解到微分符号用于表示一个变量的微小变化，而dx和dy则分别表示自变量和因变量的微小变化，它们在导数的计算中发挥着重要作用，并广泛应用于各个领域，希望本文能帮助读者更好地理解这些符号的含义及其在微积分中的应用。